Quantum Mechanics is the science of the infinitely small, conceived by a group of brilliant minds over the course of thirty years, from 1900 to 1932[1]. During this period, also in response to some unsolved problems of Classical Physics, the foundations of the most successful scientific theory ever were laid – at least in terms of agreement between predictions and experimental results.

It was immediately clear that this new science, which it would be more appropriate to generically call Quantum Physics, said something profound and fundamental about the nature of matter. First of all, it comprehensively explained the stability and characteristics of atomic structures[2]. In addition, it allowed to address some of the problems of the “new” emerging Physics of the time: radioactivity, nuclear reactions, the physics of elementary particles as well as solid state physics, to which we owe, among other things, much of the technological progress that followed.

Finally, Quantum Physics also has philosophical and epistemological aspects of great relevance and therefore a considerable impact – still under careful study – on our vision of the world.

But first of all let us start by discussing the first version of this theory, the so called Non-Relativistic Quantum Mechanics (NRQM).

[1] The first “quantum hypothesis” was formulated by Max Planck in 1900, while 1932 is the year of the discovery of the first antiparticle (the positron), as predicted by Paul Dirac quantum relativistic theory.
[2] According to Classical Electromagnetism the atom should not even exist, being an unstable system.

What is non-relativistic Quantum Mechanics?

Without any claim to review in a complete way its fascinating history, we can first of all say that NRQM is a formal theory, making use of an abstract mathematical language. The objects of this theory are not, as in the case of Classical Physics, quantities that we can borrow from everyday use in common life such as masses, accelerations, electric currents or forces. On the contrary, they are abstract entities “living” in suitable mathematical spaces. This fact has certainly contributed to forming an aura of mystery around this theory, which is probably somehow excessive.

In fact, there are no profound reasons why a physical theory must conform to our intuition or common sense; moreover, Quantum Physics mainly concerns the nature of the atom – a system that has dimensions smaller than a ten-thousandths of a micron, very far from the reach of our senses and our daily experience.

In NRQM the system (the particle) is described by means of a mathematical function in an abstract space: it is the wave function that depends both on spatial coordinates as well as other quantum degrees of freedom. The wave function evolves in the abstract mathematical space[3] and represents the quantum system. We are here in a very different situation from that of Classical Physics, because the wave function does not give any certain information about where the particle is, or where it is going, at a certain moment. And in fact, NRQM has some features that are quite distant from our common sense, above all in two aspects: its intrinsically probabilistic structure and the related Uncertainty Principle.

The intrinsically probabilistic structure of the theory is revealed in the fact that different systems prepared in the exact same way, can evolve in different ways. This fact is not familiar to us: according to our daily experience, a basketball always thrown with the same force and in the same direction will always end up in the basket following the same trajectory. If we really repeat the shots in the exact same way, the ball will always enter the basket. On the contrary, an electron “prepared” in a given state may evolve into different states, say A and B, without us being able to predict with certainty which of the two. But we will be able to say, thanks to the theory, that state A has a 30% probability and state B 70% probability of occurring[4]. The impossibility of predicting the outcome of a single event (will the electron evolve in A or in B?) is the reason why we say that the theory is inevitably characterized by a statistical aspect.

The Uncertainty Principle, another typical characteristic of Quantum Physics, denotes the fact that certain quantities cannot, in principle, be measured with arbitrary precision together. For example, we cannot know well – and simultaneously – the position and velocity[5] of a quantum particle. This is once again different from the classic case of a basketball or soccer ball. We are in fact certain that when we take a penalty kick, we know where the ball is (on the penalty spot!) and we also know its speed (equal to zero). This type of knowledge is impossible in Quantum Physics: either we know the position well (and the velocity will be uncertain), or we know the velocity well (and the position will be poorly known).

The theory features pairs of quantities that cannot be known infinitely precisely at the same time[6]. The improvement of the measurement of one quantity (for example the velocity of a particle) determines the worsening of that associated with the other quantity (position of the same particle). The uncertainties in the knowledge of position and velocity are determined by the value of Planck’s universal constant h, which characterizes the size scale of the quantum world.

Because of this fact, we cannot really say that our electron has a trajectory. Because, to have a trajectory it is in fact necessary to have (at all times!) a position and a velocity. This aspect makes the theory seem even more strange to us: we are used to thinking that the basketball follows a trajectory – which we see clearly on television – before entering the basket. But this is not the case for an elementary particle: we can never “see its trajectory”.

In fact we could somehow reverse the argument; if we want, the “magic” of Quantum Mechanics is precisely this: despite starting from principle limitations of knowledge (such as those just seen), the theory is able to yield the most accurate predictions ever formulated by human knowledge. And in a certain sense we can attribute this to the generality of his vision, to the ability to integrate two originally distant and opposing concepts: that of a wave and that of a particle[7]. In this sense, Quantum Physics features an extraordinary depth of penetration inside the inner properties of matter.

These characteristics of the theory make it truly unique in the history of Modern Physics and sharply pose the problem of its interpretation.

[3] Usually, this is one of the so-called “Hilbert spaces”
[4] These probabilities will be known with extraordinary precision, together with their evolution in time. The theory therefore features an extraordinary predictive power.
[5] To be precise, not the velocity but the linear momentum.
[6] And not even with “perfect” measuring instruments. It is an uncertainty “in principle”.
[7] It is the well known “wave-particle duality” of the theory, introduced by De Broglie in 1923.

The Interpretation of Quantum Mechanics

First of all, every physical theory is subject to interpretation, as it implicitly proposes a vision of the world: in addition to the essential predictive aspect by which the value of the theory is primarily judged[8], we are also necessarily confronted with the descriptive aspect: what does the theory say about the world? What vision of the world is promoted?

In the case of Classical Physics this vision is that of a deterministic and material world, where the elements at play are intuitively clear quantities, mechanical, optical, acoustic or fluido-dynamical, in good agreement with our space-time experiences and our “common sense”. However, it is less immediate to answer the question of which vision of the world is proposed by Quantum Mechanics, given that it makes abundant use of elements far from our experience – such as the concept of the wave function. And faced with this problem, generally speaking, two schools of thought have emerged.

The main line of thinking – generically called the “Copenhagen school” due to the role played by Niels Bohr – considers that the purpose of the theory is essentially to make predictions about the results of experiments. Without claiming to have a vision of the world that is independent of our measurements, and therefore privileging the predictive aspect over the descriptive one. In this approach, undoubtedly positivist in nature, in a certain sense the descriptive aspect of the world is largely given up. Or limited to the case in which the world interacts with us through the measurement process. This appeared unsatisfactory to many physicists – including some of the illustrious founders of the theory itself.

For these reasons, currents of thought have arisen in which it is believed that Quantum Mechanics (in addition to correctly predicting the results of experiments) should also give a somehow “more complete” vision of the world, and in particular less dependent on the role of observers and measurements. According to these scholars, the “Copenhagen-style” description of the world is unsatisfactory as there is a great imbalance between the extraordinary predictive power of the theory and its poor description of the world. Generally, thinkers in agreement with this line tend to believe that quantum indeterminacy signals its incompleteness and that somehow there exist further degrees of freedom not yet identified (the hidden variables) that, if known, could make the description more complete, satisfactory – and in particular deterministic. In this regard, Einstein’s statement “God does not play dice”[9] is famous and significant, indicating the idea that the profound nature of the physical world should be deterministic.

But in the meantime, and independently of the interpretative efforts, the theory evolved by addressing the problem of relativistic invariance.

[8] Which are the results being predicted by the theory and how much they are close to actually measured values.
[9] Literally: der Alte würfelt nicht. The Old One does not play dice.

From NRQM to Relativistic Quantum Mechanics

The amount of success achieved by this theory since its inception was very remarkable. Starting with the agreement with the results of the first experiments in atomic and nuclear physics, on the spin of the electron and the energetic structure of the hydrogen atom.

The first version of the theory, NRQM, was completed with the demonstration of the equivalence between Heisenberg’s matrix formalism and Schrödinger’s wave function approach. And complemented with Born’s probabilistic interpretation of the wave function. The formal basis of NRQM is the Schrödinger Equation of 1926, which defines the evolution of the wave function, the representative function of the quantum system.

However, at this stage of evolution the theory still showed small discrepancies with the results of the most precise experiments, discrepancies mainly due to the (well known) fact of being a non-relativistic theory. In a non-relativistic theory, the interaction between different particles propagates with infinite speed (action at a distance), in contradiction to Relativity, according to which nothing in nature can propagate with a speed greater than that of light.

The formulation of a relativistic Quantum Mechanics is due to Paul Dirac who developed, in 1928, a relativistically invariant and at the same time quantum equation. In this way, the fusion between two fundamental theories of Modern Physics was achieved: Quantum Physics and (Special) Relativity. The consequences of this unification were truly spectacular.

First of all, this new formulation of the theory required the formal description of the quantum system to be in a “larger” mathematical space, requiring a more extensive representation. And the remarkable fact was that this extension allowed to naturally predict the two properties of spin and the presence of antiparticles.

In fact, we must remember that spin was an experimental reality – recently discovered. But it did not need to exist in non-relativistic theory. It was precisely the new Dirac equation that required the existence of this quantity as “emerging” from the invariance properties of the theory.

And not only that: the Dirac equation also required the existence of antiparticles, i.e. it required for example that in addition to the electron (with a negative charge), there also existed an anti-electron of equal mass but with a positive charge[11]. This antielectron (called a positron) was actually discovered a short time after the formulation of Dirac’s theory, in 1932. This discovery, by Anderson and Neddermeyer, marked one of the greatest triumphs of Physics of all time.

This experimental prediction, formulated on the basis of the harmonization of Quantum Physics and Special Relativity, had allowed the discovery of an entire new class of particles; it was one of the many examples of the power of the theory, in apparent contradiction with its extremely abstract aspect. A fact that did not fail to arouse great amazement even in some of the protagonists of this revolution[12].

[10] Here we are skipping some pieces of historical development, namely the “Dirac sea theory” that would have been superseded with the discovery of the positron
[11] For instance, Eugene Wigner in 1927 wrote a book about it, having the significant title: “The unreasonable effectiveness of mathematics in the natural sciences”.

A new quantization

But despite the sensational progress, some difficulties remained in the new relativistic Quantum Mechanics. An important class of problems was due to the notion of causality, and were related to describing the physical system with the wave function. This function (both in Schrödinger and Dirac theories) is linked to the probability of the presence of a particle: the so-called Born interpretation. It is therefore a “single particle” description, and this fact still caused some inconsistencies.

These difficulties were overcome by the introduction of an even more abstract theory, a theory still of a quantum nature, but which considered, instead of the particle wave function, a more “general” entity, extended to all spacetime: a field. Of course, a quantized field. Particles, in this new vision, are represented by excitations of the field itself, in a formalism that respects relativistic causality[12] and naturally allows for the creation and destruction of both particles and antiparticles (matter and antimatter). For instance, the theory describes in a natural way the production of particle-antiparticle pairs in collision experiments, transforming energy and matter into each other according to the well known relativistic equation E = mc².

These processes of creation and destruction of particles and antiparticles occur in the ways permitted by Quantum Physics and can be both “real” (actual production of particles from the vacuum) and “virtual” (fluctuations compatible with the Uncertainty Principle). From this perspective, the new quantization “forces” us to attribute dynamic properties to the void, to the very structure of spacetime. This is a very important change in perspective: restricting ourselves to the field of Physics, this is the change from a merely geometric spacetime to a dynamic vacuum capable of genuine physical effects. A fact also confirmed directly by the observation of the Casimir Effect, by which two parallel metal plates placed close together attract each other due to the electromagnetic interactions caused by the quantum fluctuations of the vacuum.

This new vision of Quantum Physics, the most modern we have, is generally called “second quantization”, while the term “quantization” (or even “first quantization”) is reserved for NRQM or Dirac theory.

Quantum Physics in this version is called Quantum Field Theory (QFT) and is the most accurate vision we have of the atomic, subatomic and nuclear world. In simplified and schematic form, the relationship between the various quantum theories is shown in figure 1.

[12] The fields cannot influence each other at points in spacetime outside their respective “light cones”. This translates the fact that no physical interaction can be transmitted superluminally in Special Relativity.

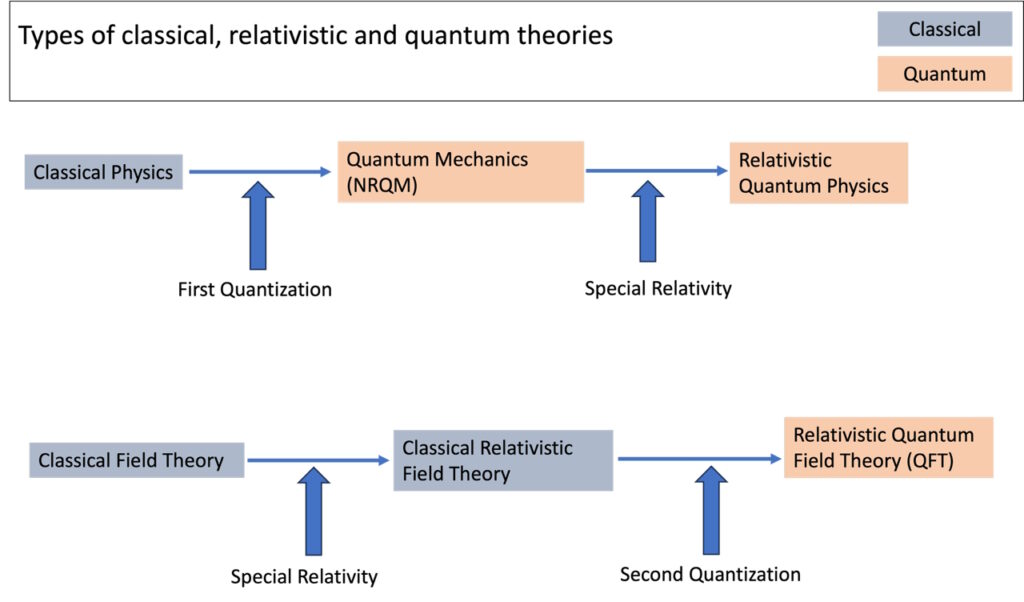
Figure 1. Functional relationships between the various forms of the theory. The most modern one we know is QFT, obtained from the quantization of a relativistic classical field theory, following a prescription called “second quantization”.

The Quantum Field Theory (QFT)

A Quantum Field Theory (QFT) starts from the definition of the fields we choose and quantizes their nature, thus including the possibility of creation and destruction of particles and antiparticles. This formalism also allows to describe in a natural way the relationship between spin and statistics. In Atomic Physics this is the Pauli Exclusion Principle: particles with spin ½, called fermions, repel, which determines the solidity of matter[13]. Furthermore, as we have already said, the theory gives the vacuum a new, special dynamic state: the vacuum is to be considered “filled” by fundamental quantum fields which, fluctuating in accordance with the Uncertainty Principle, can produce pairs of particles and antiparticles[14].

Furthermore, QFT is deeply linked to symmetry principles, both those already present in the classical field theory (Noether’s Theorem) as well as the relativistic ones (invariance with respect to the transformations of Special Relativity, i.e. with respect to the Lorentz Group). It also allows the description of the discrete symmetries C,P and T[15].

These developments highlight the ever-increasing role of symmetry principles in Physics. According to a famous phrase by Frank Wilczek, a symmetry is, in a certain sense, a difference that makes no difference. This principle becomes particularly evident with the Gauge Invariance concerning the fully relativistic entity that is the field. This property requires that the dynamics of a QFT be invariant under changes that redefine the fields of the theory itself in a certain way, according to so-called “gauge” transformations.

This symmetry has a profound dynamic meaning: starting from a theory with the simplest possibile gauge invariance (the “global” one), it is possible to enrich the dynamics with new interactions simply by requiring the most restrictive (“local”) version of the symmetry itself. The presence of physical interactions is therefore introduced by the requirement of local gauge invariance.

This link between dynamics and symmetries is one of the most important conceptual innovations of Modern Physics and this way of “generating” fundamental physical interactions in QFT using the Gauge Principle has now become a truly paradigmatic method. Gauge invariance has in fact taken the role of an almost indispensable symmetry in any advanced quantum theory[16].

There are several possible forms of QFT, and the one of greatest interest includes the fields that have actually been observed in nuclear and particle physics experiments: these are the two fields of Strong Nuclear Interactions (also called QCD from Quantum Chromodynamics) and Electroweak Interactions, which successfully describe the dynamics that take place between the most fundamental building blocks of known matter: quarks and leptons[17].

The name “Standard Model of Elementary Particles” is given to the specific form of QFT which describes the interactions between quarks and leptons in terms of the two theories of Strong Nuclear Interactions (QCD) and Electroweak Interactions. It is an astonishing intellectual construction and the results of the work and passion of many researchers over the course of almost a century.

This vision also arises from a great historical success, schematically shown in figure 2: the unification between the fields of Quantum Electromagnetism (QED, Quantum Electrodynamics) on the one hand and the Fermi theory of Weak Nuclear Interactions on the other. This unification of QED with Fermi theory is called Electroweak Unification.

[13] More correctly, two spin ½ particles cannot share the same quantum state.
[14] This creation does not violate energy conservation because one of the forms of the Heisenberg Principle links Energy and Time. Furthermore, particle-antiparticle pairs are created with opposite quantum numbers: a negative electron is produced together with a positive positron, thus respecting charge conservation.
[15] Charge inversion C, spatial inversion P and temporal inversion T.
[16] To be complete, one should say that gauge theories typically are “renormalizable”, a property that allows to mathematically handle the infinities showing up sometimes in the theory.
[17] In the case of the atom: protons and neutrons are made up of quarks, while the electron is one of the leptons.

The Electroweak Unification

The theoretical-experimental process that would lead to Electroweak Unification began in the 1960s, went through a decisive moment in 1973 with the definition of the GSW model (named after the authors Glashow, Salam and Weinberg) and then culminated with the discovery of W and Z particles at CERN[18] in 1984, obtained by the UA1 group (led by Carlo Rubbia) and by the UA2 experiment as well. In the meantime, t’Hooft and Veltman demonstrated the mathematical soundness of the new Electroweak quantum field, by proving its renormalizability.

This is undoubtedly one of the greatest successes of modern knowledge: the QED of Feynman, Schwinger and Tomonaga, and the Fermi Weak Nuclear Interaction are recognized as manifestations of the “more fundamental” Electroweak field. At high energies, this field is manifestly present but when the energy is lower[19], Electroweak Interactions split into Weak Nuclear Interactions and QED. Therefore, the three fundamental fields (Gravitation, QCD and Electroweak field) at low energy manifest themselves as four (figure 2).

Figure 2. The fundamental fields of Modern Physics, with the unification that took place between 1973 and 1984. Today it is thought that there are three fundamental fields: the strong nuclear interaction, the electroweak interaction and gravitation. All the fields in this figure are QFT-type fields, except gravitation which is represented by a classical theory (General Relativity).

It is not the first time that this has happened in Physics: a unification of fields known to all is that between Magnetism and Electrostatics – to form the Classical Electromagnetism of Faraday and Maxwell during the 19th century. But there are many other examples.

Ultimately, there are three fundamental fields, namely Gravitation and two quantum fields: QCD and the electroweak field[20]. As we have said, the type of QFT that considers quarks and leptons interacting through QCD and the Electroweak Interaction is the so-called Standard Model of Particle Physics: a theory with resounding success, capable of explaining decades and decades of experimental results obtained with the help of large accelerators such as those at Fermilab in Chicago or CERN in Geneva – but also observations obtained in the physics of particle from the Cosmos. The power of this version of modern Quantum Physics is such that its formalism must also be used in Cosmology – to correctly understand the dynamics of the first moments of the evolution of the Universe. To understand the Big Bang.

Ultimately, QFT is a decisive and fundamental part of our vision of the universe: two fundamental quantum fields that evolve in a spacetime described by General Relativity. Since the beginning of time.

[18] European Centre for Nuclear Physics, hosting the world’s biggest accelerator, the LHC (Large Hadron Collider).
[19] Below the mass of W,Z boson. That is, smaller than about 100 GeV (Giga electron-Volt).
[20] We do not yet have a quantum theory of Gravitation, as will be made clear shortly.

The unification with Gravity

The path of modern quantum theories leads us directly to new challenges, and naturally to the possibility of new unifications. The first plausible unification ahead seems to be the one between the Electroweak and QCD fields, a possibility that could (or should) occur at energies much higher than those reached by contemporary accelerators. This type of unification is sometimes called “grand unification” and the relevant theories are called GUT (Grand Unification Theories).

A GUT theory is therefore a relativistic quantum field theory that would describe all fundamental quantum interactions with a single entity (the “GUT” field). This field would then give rise to different forms of interaction within the “low energy” limit, i.e. the energies accessible in laboratories. This is an advanced research topic, on which perhaps even excessive trust is placed – however this unification seems plausible[21]. And taking the leap of faith that it is actually verified, research often focus on the “ultimate” goal of unifying all quantum physics with gravitational physics. The next step.

Undoubtedly one could object, at this point, to the meaning of a “subsequent” step when the previous case has not yet been solved. In this regard, however, let us recall that it is often precisely from a more general approach that “minor” problems can be successfully addressed. And the next step to GUT Unification has a different and deeper conceptual value; it would mean harmonizing the entire physics, unifying the quantum fields with a classical one: Gravitation – the great theory excluded from the quantum revolution.

This is the final challenge, the “Holy Grail” of modern research: understanding gravity from the quantum point of view. Being able to correctly formulate the so-called Quantum Gravity. Gravitation is in fact the only fundamental interaction still described by a classical theory[22], General Relativity, and its unification with other forces appears to be a challenging goal – despite being at the center of the efforts of many contemporary scholars.

This research is mainly addressed by means of String Theories, generically set in many-dimensional spaces. But there are also other approaches, even more speculative and daring, such as Loop Quantum Gravity or theories of geometry quantization (Fuzzy Geometry). This family of theories offers an incredible kaleidoscope of methods and tools invented by human ingenuity: from multidimensional spaces to the treatment of divergent integrals. From regularization procedures to the compactification of extra-dimensions in order to “fall back” into our world of three spatial and one temporal dimensions.

The experimental study of this physics requires energies much greater than those achievable with today’s accelerators. But perhaps the Universe can help us: phenomena such as the coalescence of Black Holes or Neutron Stars (which generate Gravitational Waves) or Supermassive Black Holes (millions of solar masses) could provide valuable information on quantum aspects of gravitation. Systems of this type, recently discovered, are capable of concentrating a very high gravitational energy and generate strong spacetime curvatures and possible quantum effects.

Undoubtedly, the challenges of knowledge never end.

[21] It must be emphasized that this unification has not been proven, in spite of the exaggeratedly optimistic statements often found in popular literature.
[22] In the sense of “non quantum”, and NOT in the sense of “non-relativistic”. General Relativity is (obviously) relativistic.

A vision of the world

The most radical innovation of any new form of knowledge is probably that of impacting our vision of the world, of changing it in some sense. This is certainly the case of Quantum Physics. The successes of this theory are so striking that we can today define it as a “meta-theory”, thus elevating it to the role of a “mode of constructing theories”. In the sense that a specific physical theory or model is improved precisely if it is developed taking quantum effects into account, i.e. in fully quantum mode. In other words, the “being quantum” of a theory represents an improvement, realizing a fuller and more fundamental way of being a model. A way to “turbocharge” our physical theory.

As expected, there are aspects of QFT that have significant epistemological implications, naturally with regards to its interpretation. But what is the interpretation of a physical theory? In simple words, as we have said before, it is the answer to the question “What does this theory tell us about the world?” And every far-reaching physical theory “must” tell us something about the world[23]. This is what we previously called the descriptive aspect of the theory.

In the case of Quantum Physics the answer is to be considered somehow delicate, because it simultaneously tells us something “about the world” but also about ourselves in relation to the world. And this is why its interpretation is still the subject of discussion today among experts, both physicists and philosophers of science. But also among enthusiasts of all kinds.

This discussion, it is worth noting, begins immediately. It begins with the emergence of the first version of the theory, the NRQM: an intense debate immediately arises involving the very founders of  the theory and the philosophers of science (for example of the Vienna Circle). And whose best-known culmination is the very famous “debate between Bohr and Einstein”.

The most relevant consequence of the theory concerns precisely the relationship between us and the world, between observer and observed system. Between subject and object. This is also because in some key experiments of Quantum Mechanics a vision that physicists had implicitly assumed since the times of Galileo and Newton is put into serious difficulty: that of realism.

Realism in physics generally starts from the assumption that any system can be studied without disturbing it, or by reducing to a minimum (ideally reducing to zero) the perturbation induced by the measurement. According to the realist vision, the system evolves completely independently of our intentions, independently of whether we decide to observe it or not: all physical quantities exist and evolve regardless of whether they are measured. It follows that each measurement represents a simple “recording” of facts, with are not influenced (at least in principle) by the action of the observer. However, all this does not apply to an electron or to any other system where quantum effects are important.

In Quantum Physics it is not possible to conceive a physical system as rigorously distinct from the operations we carry out to study it: the system will always be influenced by our measurement and, in some sense “it exists” only when we measure it. Without the measurement we could not, strictly speaking, even speak of its properties as “existing”. This is an extremely different condition from that of a “classical” (non-quantum) system: in classical physics no one doubts that a forcefully thrown soccer ball has a certain speed – regardless of how the speed is measured. Or regardless of whether it is measured at all. But for an electron it is different.

For an electron, the value of the measurement result is determined by the measurement itself and its modalities: at a certain quantum level, its properties are inseparable from the measurement process itself. Observer and observed become inextricably linked, subject and object cannot be fully distinguished. And this is the challenge that Quantum Physics poses to all human knowledge. To his vision of the world.

To highlight these effects it is necessary to carry out experiments in which the quantum nature of the system is particularly evident. The results of these class of experiments are now very many and incontrovertible[24]. And they lead us to a new vision of the world. And of ourselves in the world.

However, it is important to note that this scientific and philosophical debate is still conducted almost exclusively by considering the first version of quantum theory, the NRQM. This is, largely, the only version of the theory that has been disseminated, popularized, and widely known to philosophers. And in this form[25] the theory has given this extraordinary epistemological lesson.

However, there are other, more modern forms, of Quantum Theory, such as the QFT. And it is precisely in the field of QFT that the philosophical debate has recently begun, with truly new and interesting implications[26] which involves both philosophers of science and physicists passionate about epistemological aspects.

In fact, as we have seen, QFT is a rather different theory from the Quantum Mechanics of the first decades of the last century, and presents new conceptual features – while maintaining some of the initial characteristics. As we have seen, in QFT the fundamental entities are quantum fields, from which the possibility of creating particles and antiparticles and the dynamic structure of the vacuum derives. It is therefore not surprising that QFT has also led to a new language, of which the most obvious example is that of Feyman diagrams, which appear in many of its aspects[27].

And this language inevitably changes our vision of the world once again.

[23] The case of Newtonian Gravity is a very clear example.
[24] These are generally experiments in which a “Bell” type inequality can be formulated, and it is possible to perform an experiment of the type of the historic experiment by Aspect and collaborators.
[25] We should say for completeness that even in the specific form of Quantum Optics (also relativistic), the theory has given the same type of answers to the epistemological questions we have mentioned.
[26] See for example: D.J. Baker – The Philosophy of Quantum Field Theory – The Oxford Handbook of Topics in Philosophy, 2014. https://doi.org/10.1093/oxfordhb/9780199935314.013.33.
[27] In particular in the case of perturbative calculations.

Autore: Marco Giammarchi e Marco Torri